Synopsis Computations on binary trees.
Description We consider binary trees---trees with exactly two children---that have integers as their leaves.
Our trees can have red and black nodes and we want to perform the following operations on them:
- Count the number of red nodes.
- Compute the sum of all the integers that occur in the leaves.
- Extend the tree data type with green nodes.
- Replace all red nodes by green ones.
Examples The definition of ColoredTrees is as follows:
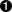 ) we define the data type of
) we define the data type of 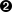 ) counts all red nodes by visiting all nodes and incrementing
the counter
) counts all red nodes by visiting all nodes and incrementing
the counter  ) visits all nodes and adds the integers in each leaf node.
In
) visits all nodes and adds the integers in each leaf node.
In 
 ) visits all nodes and turns red nodes in green ones.
) visits all nodes and turns red nodes in green ones.
We can now explore ColoredTrees:
module demo::common::ColoredTrees // Define ColoredTrees with red and black nodes and integer leaves data ColoredTree = leaf(int N)First (| red(ColoredTree left, ColoredTree right) | black(ColoredTree left, ColoredTree right); // Count the number of red nodes public int cntRed(ColoredTree t){ int c = 0; visit(t) { case red(_,_): c = c + 1;
}; return c; } // Compute the sum of all integer leaves public int addLeaves(ColoredTree t){ int c = 0; visit(t) { case leaf(int N): c = c + N;
}; return c; } // Add green nodes to ColoredTree data ColoredTree = green(ColoredTree left, ColoredTree right);
// Transform red nodes into green nodes public ColoredTree makeGreen(ColoredTree t){ return visit(t) { case red(l, r) => green(l, r)
}; }
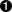 ) we define the data type of
) we define the data type of ColoredTrees with constructors
leaf, red and black.
cntRed (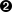 ) counts all red nodes by visiting all nodes and incrementing
the counter
) counts all red nodes by visiting all nodes and incrementing
the counter c for each red one.
addLeaves ( ) visits all nodes and adds the integers in each leaf node.
In
) visits all nodes and adds the integers in each leaf node.
In 
coloredTrees are extended with a new constructor green.
makeGreen ( ) visits all nodes and turns red nodes in green ones.
) visits all nodes and turns red nodes in green ones.
We can now explore ColoredTrees:
rascal>import demo::common::ColoredTrees; ok rascal>rb = red(black(leaf(1), red(leaf(2),leaf(3))), black(leaf(3), leaf(4))); ColoredTree: red( black( leaf(1), red( leaf(2), leaf(3))), black( leaf(3), leaf(4)))Count the red nodes in
rb:
rascal>cntRed(rb);
int: 2
and compute the sum of all leaves:
rascal>addLeaves(rb);
int: 13
Finally, we convert all red nodes:
rascal>makeGreen(rb);
ColoredTree: green(
black(
leaf(1),
green(
leaf(2),
leaf(3))),
black(
leaf(3),
leaf(4)))
Benefits This example illustrates the fully automatic visiting of the elements of a structured data type.
Compare this with the traditional programming style in which a switch statement is used to determine
the constructor and recursion is used to visit substructures. This style becomes particularly cumbersome
for data types with large numbers of constructors such as, for instance, abstract syntax trees for real
programming languages.
Pitfalls The visit statement is based on a new paradigm one has to learn.